Area of Rhombus

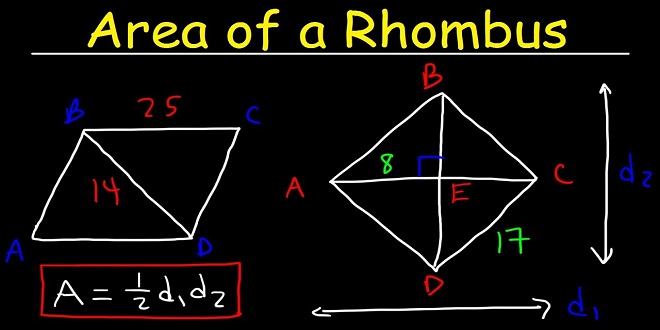
A rhombus can be defined as a two-dimensional or 2D plane figure which has an enclosed shape or structure. The area of a rhombus is being considered a special type of parallelogram. Also, to note that for its unique properties, the rhombus also gets a self-identity as a quadrilateral structure. The Rhombus is also known as the equilateral quadrilateral, this is because of the meaning of ‘equilateral’ which means all of its sides are always equal in length. ‘Rhombus’ this term has been rightfully derived from the ancient Greek word called ‘rhombus’, this word means something which spins. The area of rhombus can be found as ½ * diagonal 1 * diagonal 2.

Rhombus Is Actually a Parallelogram

A rhombus is perfectly defined as a unique parallelogram because of its requirements of being a parallelogram, this is also a quadrilateral that has two pairs of parallel sides. Additionally, a rhombus also has a set of four equal sides, but this is even a type of parallelogram that has four sides as congruent. Thus, a rhombus will fit all its basic properties of being a parallelogram. We will notice the properties of a parallelogram in its four sides remaining the same length and its opposite sides as remaining parallel enough.

Methods of Calculating the Area of a Rhombus

The area of a rhombus is defined as the amount of space that is being enclosed by the rhombus in a two-dimensional space. Let’s recall, this as a rhombus, which is a type of a projected as the two-dimensional or a 2D plane, which have four sides which have an equal side of length and is a congruent side.

The methods which help us in calculating the area of a rhombus will be explained below with the help of the methods and steps. There will exist three methods that help us in calculating the area of a rhombus, they are as follows:

Method 1: This is done by using the diagonals

Method 2: This is done using the base and height

Method 3: This is done using the trigonometry

Steps for calculating the area of a rhombus by method 1 is as follows:

Step 1: Firstly, we need to determine the length of the diagonal, which is the distance between the sides A and C. Then the diagonals of a rhombus are exactly perpendicular to each other, this by making the 4 right triangles after they intersect each other at the center of the rhombus.

Step 2: Now let us find out the length of the diagonal, that is which is the distance between B and D points.

Step 3: Then multiply both these diagonals, d₁, and d₂.

Step 4: Then divide the result by the number 2.

Rhombus

As defined earlier, a rhombus is a 2D or two-dimensional plane figure which has a closed shape. This is being considered as a special parallelogram, for all of its unique properties, this gets an individual identity which is the quadrilateral form. The rhombus is also known as the equilateral quadrilateral, as equilateral means that all of the sides of the rhombus are equal in measurement length-wise.

What are the Properties of a Rhombus?

A rhombus is said to have a perfect reflection symmetry that is over both of its diagonals. Thus, now we will point out the general properties of a parallelogram rhombus, these are as follows:

• The opposite angles are always congruent or said to be equal in measurement.
• The side’s opposite sides are equal and parallel to each other.
• The diagonals bisect each other even.
• The sum of any two adjacent or the consecutive angles of the structure is equal to 180°.

Thus, we have learned about the rhombus. Like any other geometric shape, a rhombus has properties that are very unique to it. These properties help this structure to be a distinct type from the rest of the geometrical figures.

If you are curious to learn about more other figures, visit straight Cuemath and learn amazing concepts interactively.